Volume of a Triangular Prism

Volume calculator for a triangular prism

Description, how many faces, edges and vertices are there in a triangular prism

The triangular prism, is a solid that, if we make a cross section, maintains the shape of a triangle throughout its length.

It has 5 faces, 2 faces are at the ends of the shape and both are considered bases; the two identical bases are parallel and identical triangles. In case these bases are not exactly aligned then we are in the presence of an oblique prism, and if the bases are not parallel then it is not a prism. It has 9 edges and 6 vertices.

Examples of a triangular prism

We can find many objects that look like a triangular prism, examples of triangular prism shaped objects are: Inside of a kaleidoscope, that's right, most kaleidoscopes have a triangular prism inside, made of mirrors that make the image multiply itself to a hexagon. Another interesting place we can find this shape is on the cover of the album Dark side of the Moon by Pink Floyd. Can you think of any other examples? leave a comment in the comment section at the bottom of the page.

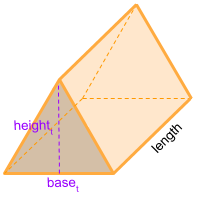
Formula for the volume of a triangular prism

To calculate the volume of a triangular prism you can use the formula for all prisms, where the area of the base is multiplied by its length. In this case the base of the triangular prism is a triangle, therefore you need to calculate the area of the triangle. You can also use the online calculator to calculate the volume of a triangular prism automatically.

Volume of other shapes

Volume of different geometric shapes: