Volume of a Hexagonal Prism
Volume calculator for a hexagonal prism
Description, how many faces, edges and vertices are there in a hexagonal prism
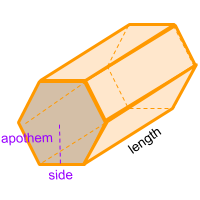
The hexagonal prism, is a figure formed by 8 faces, 2 of which are equal and parallel hexagons, and form the bases at the ends of the figure. Another 6 faces are parallelograms. It also has 18 edges and 12 vertices. If a cross section is made in any part of its length, it always maintains the shape of a hexagon.
Formula for the volume of a hexagonal prism
To calculate the volume of a hexagonal prism you can use the formula for all prisms, where the area of the base is multiplied by the length of the prism. In this case, the base of the hexagonal prism is a hexagon, therefore, the area of the hexagon need to be a known value.
To calculate the area of the hexagon (base area), multiply the perimeter of the hexagon by its apothem and divide in two. Finally to get the volume of the hexagonal prism multiply the result by the length of the prism.
Remember that the apothem is the distance from the center of the polygon (hexagon) to the middle of one of its sides. And also remember that the perimeter of a hexagon is the sum of all its sides. You can also use the online calculator to calculate the volume of the hexagonal prism automatically.
Formula explanation and alternative formula:
The formula to calculate the volume of prism is always the same:
Volume prism = Area base × Length
In this case, the area of the base of the hexagonal prism is a hexagon:
To calculate the perimeter:
Perimeter = 6 × Side
Replacing the perimeter formula in the formula shown above, then you get the main formula.
To get the volume of a hexagonal prism without knowing the apothem:
Therefor, another way to get the volume of a hexagonal prism without knowing the apothem is:
Volume of other shapes
Volume of different geometric shapes:
