Volume of a Trapezoidal Prism
Volume calculator for a trapezoidal prism
Description, how many faces, edges and vertices are there in a trapezoidal prism
The trapezoidal prism, has 6 faces, 2 of those are trapezoids and form the bases at each end of the prism, these are parallel faces, it has 12 edges and 8 vertices. If we make a cross section in any part of its length, maintains the figure of a trapezoid at the bases.
Examples of a trapezoidal prism
We can find many objects that look like an trapezoidal prism, examples of trapezoidal prism shaped objects are: some school desks that are trapezoidal in shape, but since they have thickness they need to be classified as trapezoidal prisms. Another object that is sometimes considered as a trapezoidal prism are the classic gold bars we see in Hollywood movies, but in reality they are not. The gold bars have slanted sides, therefore the shape is classified as a truncated rectangular Pyramid.Can you think of any other examples? leave a comment in the comment section at the bottom of the page.
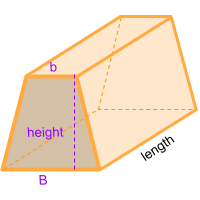
Formula for the volume of a trapezoidal prism
To calculate the volume of a trapezoidal prism you can use the formula for volume of all prism, where the area of the base is multiplied by its length. In this case the base of the trapezoidal prism is a trapezoid, therefore the area of the trapezoid that forms the base is multiplied by the length. To get the area of a trapezoid you need to sum the short and long base of the trapezoid and divide the sum by 2, then multiply by the height of the trapezoid and finally multiply by the length of the prism. You can also use the online calculator to calculate the volume of the keystone automatically.
Formula explanation:
The formula to calculate the volume of prism is always the same:
In this case, the area of the base of the trapezoidal prism is a trapezoid
Replacing the calculated area in the formula for volume of prisms we get the formula shown above.
Volume of other shapes
Volume of different geometric shapes:
