Volume of an Oblique Cone
Volume calculator for an oblique cone
Description, how many faces, edges and vertices are there in an oblique cone
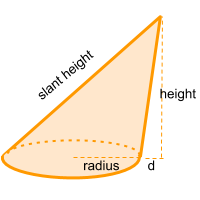
The oblique cone is the same solid shape as the regular cone, it has two faces, a circle as a base, and a curved face, one vertex (the tip of the cone) and one edge. The difference between the oblique cone and the regular cone is that its vertex is not aligned in the center. In other words, the vertex does not form a 90 degree angle with the center of the base.
Therefore when the cone has its vertex right in the middle of the base it is called a regular cone, in the case that the vertex is aligned to another side that is not the center of the base, it is called an oblique cone. In case the vertex moves outside the space of the base, it is necessary to calculate the height with respect to the same base, always keeping the angle of 90 degrees.
Formula for the volume of an oblique cone
The same formula to calculate volume is used for both the regular cone and the oblique cone. You need π (Pi = ~ 3.14) over 3, then multiply by the radius to the power of two and finally multiply by the height.
If you don't know the height or the radius, you can use the slant height to obtain some of the other data, this using the Pythagorean theorem. You can also use the online calculator to get the volume of a oblique cone automatically .
radio = √ slant height² - height² / 2
slant height = √ height² + ((2 × radius) + d)²
Volume of other shapes
Volume of different geometric shapes:
